Klassifikation

Anstatt stochastischen Konvergenzen wollen wir uns lieber mit den wirklich schweren Themen befassen. Klassifikation von Daten / Merkmalen.

Wir teilen sie einmal auf in:

• Diskret
• Stetig

und in:

• Nominal: Das Merkmal z.B. Farbe, kann nicht geordnet werden, es kann nur unterschieden werden.
• Ordinal: Das Merkmal z.B. Schulnoten kann verglichen werden, es kann also eine Ordnung hergestellt werden.
• Metrisch
  • Kardinal: Das Merkmal ist vielfaches einer Grundeinheit. z.B. Fußballfelder bei Galileo (nicht immer aber anschaulich)
  • Intervall: Nullpunkt willkürlich, z.B. Temperatur
  • Ratio: Nullpunkt festgelegt, z.B. Länge, Kelvin

Statistik

Wir kriegen Werte $x_1, ..., x_n$ gegeben...

Ordnungsstatistik

Eine Ordnungsstatistik sind $x_{(1)}, ..., x_{(n)}$ Werte, die nach Größe sortiert wurden. Z.B. $x_1 = 2, x_2 = 1, x_3 = 3$. Hierzu ist die Ordnungsstatistik: $x_{(1)} = x_2 = 1, x_{(2)} = x_1 = 2, x_{(3)} = x_3 = 3$.

So können wir den Median einfach bestimmen:

• n ungerade: $x_{(\frac{n+1}{2})}$
• n gerade: $[x_{\frac{n}{2}}, x_{\frac{n}{2} + 1}]$ (bei metrisch skalierten Daten einfach die Mitte nehmen)

Histogramm und Gruppen

Klassifiziere die Werte in Gruppen: $l_1, ..., l_k$. Die Gruppen sind disjunkt. z.B. Wir haben Noten gegeben $1.0: 5, 1.3: 2, 1.7: 1$ Dann nimmt man die Gruppen $[1.0, 1.3), [1.3, 1.7), [1.7, 2.0)$ und die beiden Randgruppen mit.

Dann gibt es die relative Häufigkeiten: für Gruppe $1$ ist die relative Häufigkeit $\frac{5}{8}$, für Gruppe $2$ $\frac{2}{8}$ und für Gruppe $3$ $\frac{1}{8}$.

Ein Histogramm ist dann einfach ein Balkendiagramm mit Höhe $\frac{f_i}{b_i}$ und Breite $b_i$. Die Breite ist natürlich die Breite der Gruppe.

Wir können auch hier eine Häufigkeitsdichte oder Dichteschätzer Funktion notiert $\hat{f}(x)$ erstellen:

$\hat{f}(x) = \begin{cases} 0 & x < 1 \\ \frac{\frac{5}{8}}{0.3} & x \in [1.0, 1.3] \\ \frac{\frac{2}{8}}{0.3} & x \in (1.3, 1.7] \\ \frac{\frac{1}{8}}{0.3} & x \in (1.7, 2.0] \\ 0 & x > 2.0 \end{cases}$

Der Erwartungswert ist dann ja einfach Mittelwert und Varianz kann mit Verschiebungssatz leichter sein.

Quantile

Das $p$-Quantil ist der Wert $x_p$ mit $P(X \leq x_p) = p$.

• $np$ ganzzahlig: Jede Zahl aus $[x_{(np)}, x_{(np+1)}]$
• sonst: $\~{x}_p = x_{\lfloor np \rfloor +1}$

Qua r tile sind die Quantile: $Q_1 = \~{x}_{0,25}, Q_2 = \~{x}_{0,5}, Q_3 = \~{x}_{0,75}$

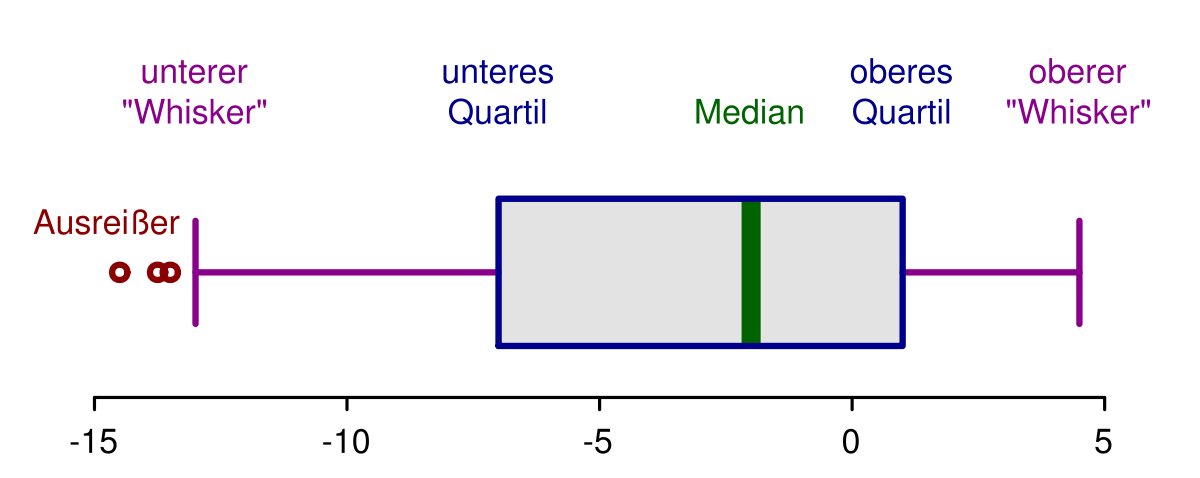
Boxplot

Aus Mittelwert / Erwartungswert, Median, Quartile, $x_{max}$, $x_{min}$ macht man dann Grafik: